云调度和DRL论文中 待解决 思考:
1.网格计算[^云计算前身]
这种计算模式是利用互联网把分散在不同地理位置的电脑组织成一个“虚拟的超级计算机”,其中每一台参与计算的计算机就是一个“节点”,而整个计算是由成千上万个“节点”组成的“一张网格”。
网格计算的优势有两个:一个是数据处理能力超强;另一个是能充分利用网上的闲置处理能力。
它研究如何把一个需要非常巨大的计算能力才能解决的问题分成许多小的部分,然后把这些部分分配给许多计算机进行处理,最后把这些计算结果综合起来得到最终结果。
2.1 P VS. NP(Nondeterministic Polynomial time)
| P | VS. | NP |
|---|---|---|
| 能快速求解(易解) | 不一定能快速求解(易验证) | |
| P一定是NP,易算易验证 | NP则不一定是P,能验证不一定能计算,如质数分解 | |
| P就是能在多项式时间内解决的问题(算的快) | NP就是能在多项式时间验证答案正确与否的问题(验证快) |
P=NP?
N即不存在不能快速求解。P是否等于NP实质上就是在问,如果对于一个问题我能在多项式时间内验证其答案的正确性,那么我是否能在多项式时间内解决它?
NP-hardness(困难) 和 NP-completeness(完全):
如果任意一个NP的问题都可以多项式[^归约]到L(L是转化后的问题,高级,困难),称问题L是NP-hard:
显然NP-hard不一定是NP问题,NP-hard是个新问题。
如果一个NP-hard,即归约后问题L本身就是NP的,则称L是NP-completeness.(NPC最难,[^时间复杂度最高])
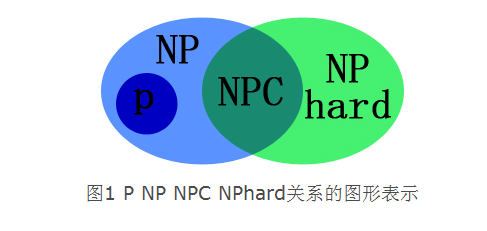
“P vs NP”问题:请问那些需要非确定性图灵机(超能力计算机)在多项式时间才能解决的问题,能够用确定性图灵机(普通计算机)在多项式时间解决吗? P vs NP不重要
2.2[^维度诅咒]
当维度增加(太大)时,体积(难度)指数增加的难题.
分类器中:
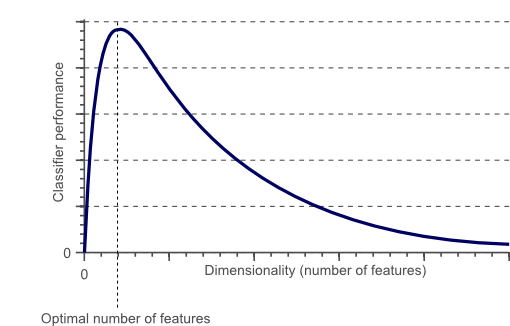
图2中随着维度的增加,分类器的性能会提高,直到达到最佳要素数。进一步增加维度而不增加训练样本的数量导致分类器性能的降低。 过拟合 ,
维度的诅咒使得训练数据的 稀疏性 ,训练样本的密度呈指数下降。
维度诅咒的另一个影响是,这种稀疏性不是均匀分布在搜索空间上。实际上,原点周围的数据(在超立方体的 中心 )比搜索空间的 角落 中的数据要稀疏得多。
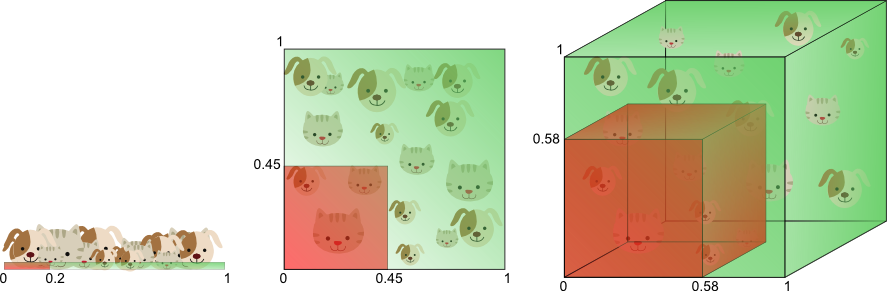
**图3.**随着维度的增加,更大比例的训练数据驻留在要素空间的 角落 中。
如何避免:
问题是 “太大” 意味着什么: [^特征的数量和样本数量有关]
特征选择方法:通常采用启发式(如GA算法)(贪婪方法,最佳优先方法等)来定位最佳数量和特征组合
特征提取方法(降维):主成分分析(PCA),它产生原始N特征的不相关的线性组合。PCA试图找到较低维度的线性子空间,以便保持原始数据的最大方差(向着极大无关组出发)。但是,请注意,数据的最大差异不一定代表最具辨别力的信息。
交叉验证:
交叉验证方法将原始训练数据分成一个或多个训练子集。
在分类器训练期间,一个子集用于 测试 所得分类器的准确度和精度,而其他子集用于 参数估计 (真实训练)。
如果用于 训练 的子集的分类结果与用于 测试 的子集的结果大不相同,则过度拟合正在发挥作用。
如果只有有限数量的训练数据可用,则可以使用几种类型的交叉验证,例如k折交叉验证和留一交叉验证。
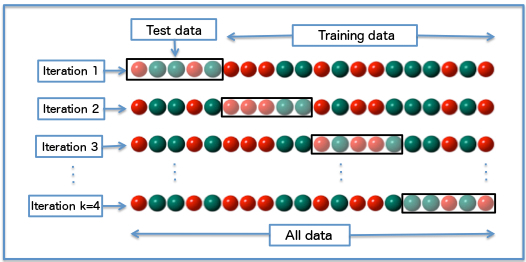
Diagram of k-fold cross-validation with k=4
为什么说RL与深度神经网络结合可以避免维度之咒?
因为神经网络能够提取特征。
Particularly in cloud computing, similar to its predecessors such as grid computing, various job assignment algorithms and approaches have been proposed [7], [8].
事实上,SVM及 神经网络 都可以看做是寻找一个合适的特征维度的过程。
当数据的维度过小的时候,数据分布过于稠密,不能很好的进行区分,这时候可以通过带有核函数的SVM将低纬度的数据映射到高纬度。
当样本的维度过大时,受限于样本的多少及计算机的计算能力,需要利用 神经网络 对样本的维度进行压缩,便于分类。
两者目的都在于使得数据的维度达到一个合适的稠密程度,从而更方便找到分类超平面。这也决定了SVM适用于低维小样本数据,而神经网络适合于大规模高维数据。
时间复杂度决定了模型的训练/预测时间。如果复杂度过高,则会导致模型训练和预测耗费大量时间,既无法快速的验证想法和改善模型,也无法做到快速的预测。
空间复杂度 决定了模型的参数数量。
由于维度诅咒的限制,模型的参数越多,训练模型所需的数据量就越大,而现实生活中的数据集通常不会太大,这会导致模型的训练更容易过拟合。
空间复杂度(访存量),严格来讲包括两部分:总参数量 + 各层输出特征图。
- 参数量:模型所有带参数的层的权重参数总量(即模型体积,下式第一个求和表达式)
- 特征图:模型在实时运行过程中每层所计算出的输出特征图大小(下式第二个求和表达式)
公式来源:卷积神经网络复杂度分析
3.梯度下降和神经网络的关系
[深入浅出–梯度下降法及其实现](深入浅出–梯度下降法及其实现 - 简书 (jianshu.com))
[深度学习] [梯度下降]用代码一步步理解梯度下降和神经网络(ANN)
matplotlib模块数据可视化-3D图
4.核心困难:云计算中多目标资源调度QoS
方法:某深度强化学习
传统方法的数学推导:
5.理论方法:
- 排队论
- 控制论
- 博弈论
6.启发式方法
- Biological Inspiration (BI): Genetic Algorithm (GA)[8],[12], [18],[20] ,Memetic Algorithm (MA), Lion Algorithm (LA)[21], Imperialist Competitive Algorithm (ICA), etc.
- Swarm Intelligence (SI): Ant Colony Optimization (ACO)[9], [19]Particle Swarm Optimization (PSO)[11],[13],[14],[15], [16],[17] Simulated Annealing (SA), Artificial Bee Colony (ABC)[22], Cat Swarm Optimization (CSO)[23], Bat Algorithm (BA), Wind Driven Optimization (WDO), etc.
新待看:
注脚:
[^归约]: polynomial-time Karp’ reduction;A转化成B问题,B至少不比A容易
[^时间复杂度最高]: 所以completeness 的直观解释就是,解决了它就可以解决所有同级别此类问题。
[^维度诅咒]: Moreover, to avoid the curse of dimensionality of traditional RL techniques, RL combined with deep neuralnetwork (i.e. DRL) is adopted in our work.
[^特征的数量和样本数量有关]: 如果N个训练样本足以覆盖单位区间大小的1D特征空间,则需要N ^ 2个样本来覆盖具有相同密度的2D特征空间,并且在3D特征空间中需要N ^ 3个样本。换句话说,所需的训练实例数量随着使用的维度数量呈指数增长。
[^云计算前身]: Particularly in cloud computing, similar to its predecessors such as grid computing, various job assignment algorithms and approaches have been proposed [7], [8].
2020/12/11

